Moving 3D Taylor-Green vortex

In this tutorial we will consider the classical Taylor-Green problem in 3D as described by Taylor and Green [TG37], with moving boundaries. The problem solves the N-S equations in the absence of body forces, and is commonly used to study transitional and turbulent flows. The problem initializes the solution at the two previous time steps, and applies periodic boundary condition on the domain walls in all coordinate directions. The problem is implemented in the file MovingTaylorGreen3D.py .

Problem description

The Taylor-Green vortex has an initial state solving the three-dimensional incompressible Navier–Stokes equations in the absence of body forces, \(\mathbf{f} = 0\), namely:

(11)\[\begin{split} \mathbf u(\mathbf x,t = 0) &= (u(\mathbf x),v(\mathbf x),w(\mathbf x))\\ u(\mathbf x) &= + \sin(x) \cos(y) \cos(z) \\ v(\mathbf x) &= -\cos(x) \sin(y) \cos(z) \\ w(\mathbf x) &= 0 \\ p(\mathbf x,t=0) &= \frac{1}{16}(\cos(2x) + \cos(2y)) (\cos(2z) + 2).\end{split}\]

The domain boundaries are prescribed a movement described by the following mesh motion from Fehn et al. [FHWK21]:

(12)\[\begin{split} \mathbf x(\mathbf X,t) &= \mathbf X + A_0 \sin \left(\frac{2 \pi t}{T_G}\right) \begin{pmatrix} \sin \left(2\pi \frac{X_2 + L / 2}{L}\right) \sin\left(2\pi \frac{X_3 + L / 2}{L}\right) \\ \sin\left(2\pi \frac{X_1 + L / 2}{L}\right) \sin\left(2\pi \frac{X_3 + L / 2}{L}\right) \\ \sin\left(2\pi \frac{X_1 + L / 2}{L}\right) \sin\left(2\pi \frac{X_2 + L / 2}{L}\right) \end{pmatrix}\\ \mathbf w (\mathbf X, t) &= \frac{\partial \mathbf x}{\partial t}\end{split}\]

where \(\mathbf X = (X_1, X_2, X_3)\) are the ALE coordinates, \(A_0=\pi / 6\) is the amplitude, and \(T_G=20\) is the period. Further parameters include the total simulation time \(T\), and \(L=1\) describing the height, width, and depth of the box mesh. By default, the Reynolds number is set to \(\text{Re} = 1/\nu = 1600\).

(HPC) Simulation in OasisMove

To simulate this flow problem in OasisMove using the default parameters, run the following command:

$ oasismove NSfracStepMove problem=MovingTaylorGreen3D

and the simulation will start. Since this problem is in three dimensions, there will be an additional set of equations to solve compared to the 2D problems in the previous demos, and consequently the simulation may take some time. To speed up the simulation, you can solve the problem using parallel computing with MPI, which OasisMove supports. Thus, to decrease the computational time by utilizing high performance computing and parallelization of OasisMove, can run the following command:

$ mpirun -np 16 oasismove NSfracStepMove problem=MovingTaylorGreen3D

Results

When the simulation is finished, there will be a folder named results_moving_taylor_green_3d, in the current working directory. Running the Taylor-Green vortex problem with the default parameters should produce the velocity and pressure solution files located in the Solutions folder: velocity.xdmf, and pressure.xdmf, which can be visualized in ParaView or a similar visualization software. In Fig. 8 we display the temporal deformation of the mesh, and the velocity field from \(T=0\) to \(T=5\).

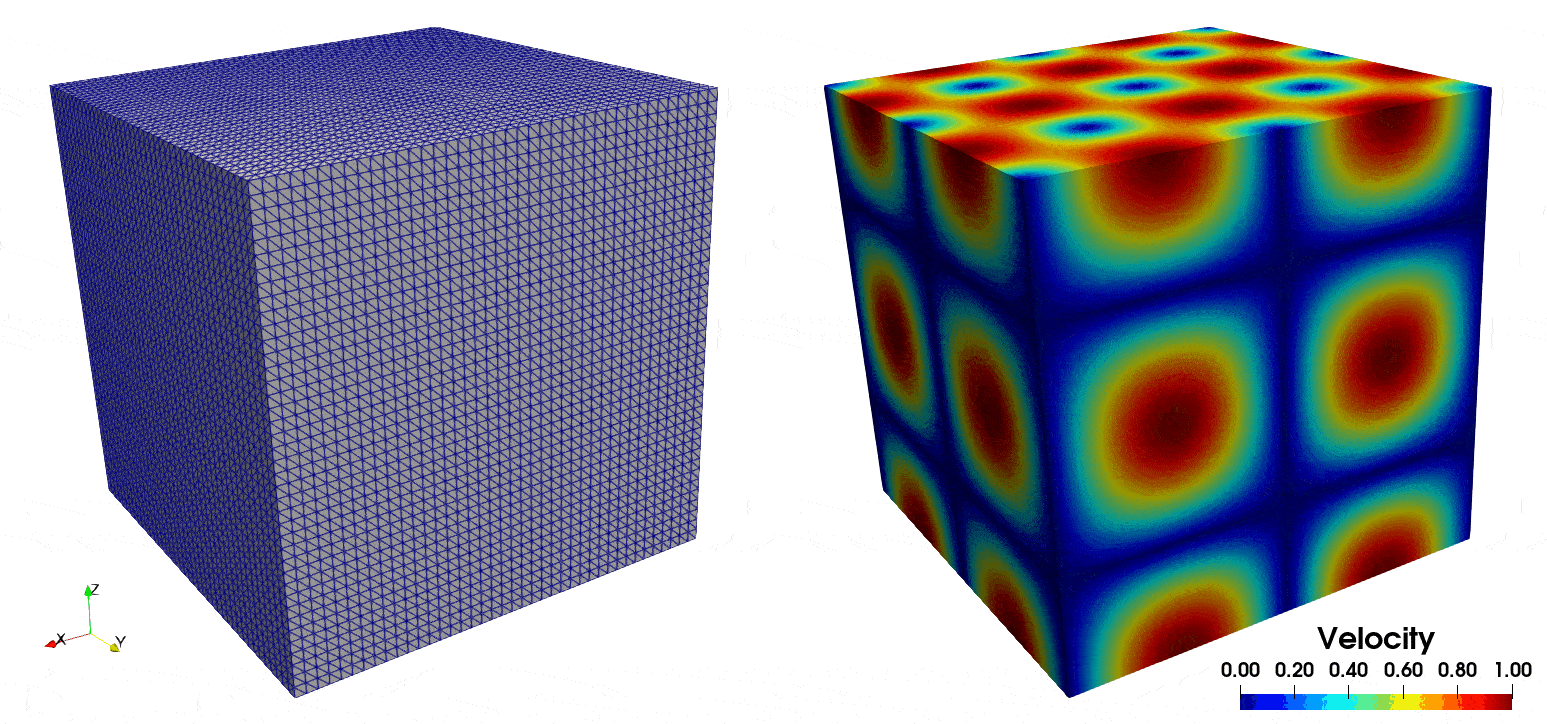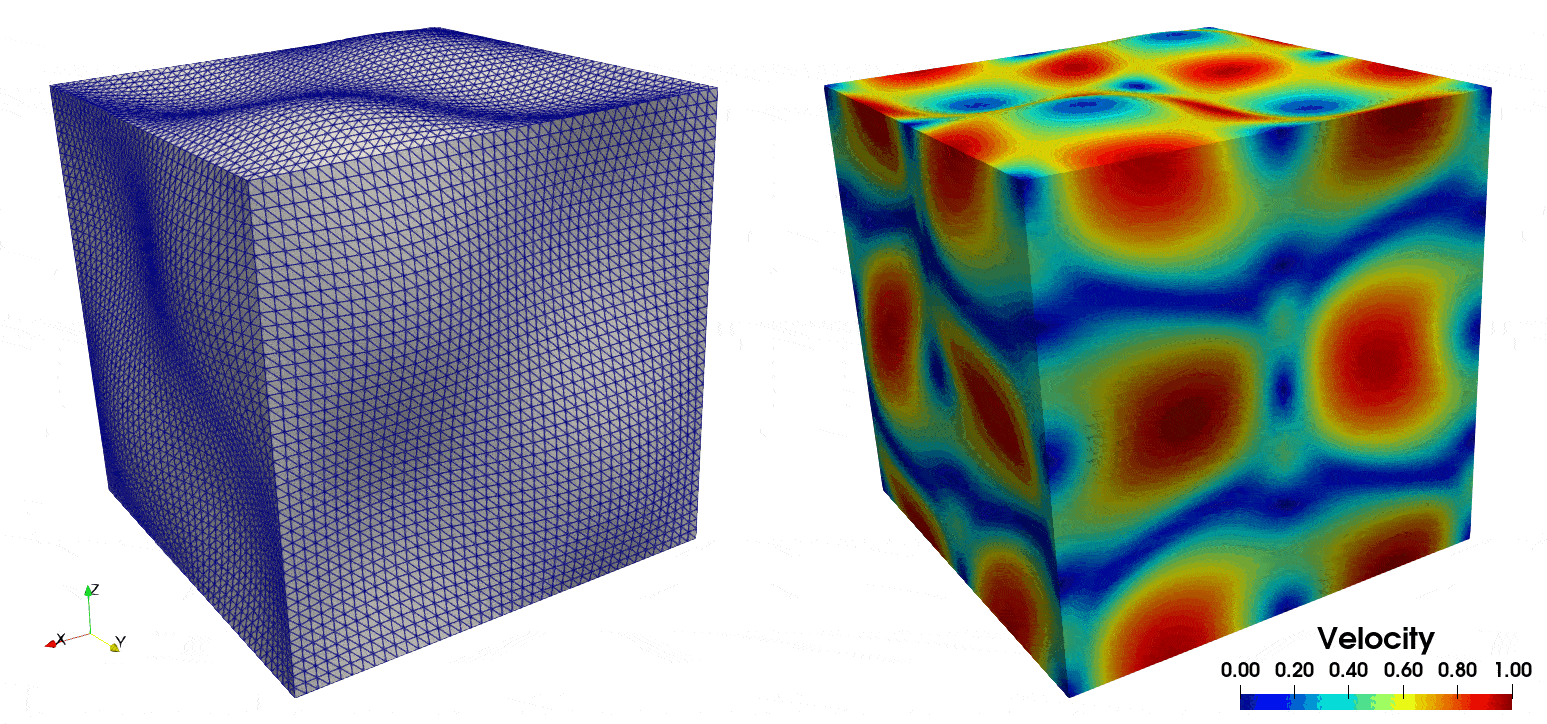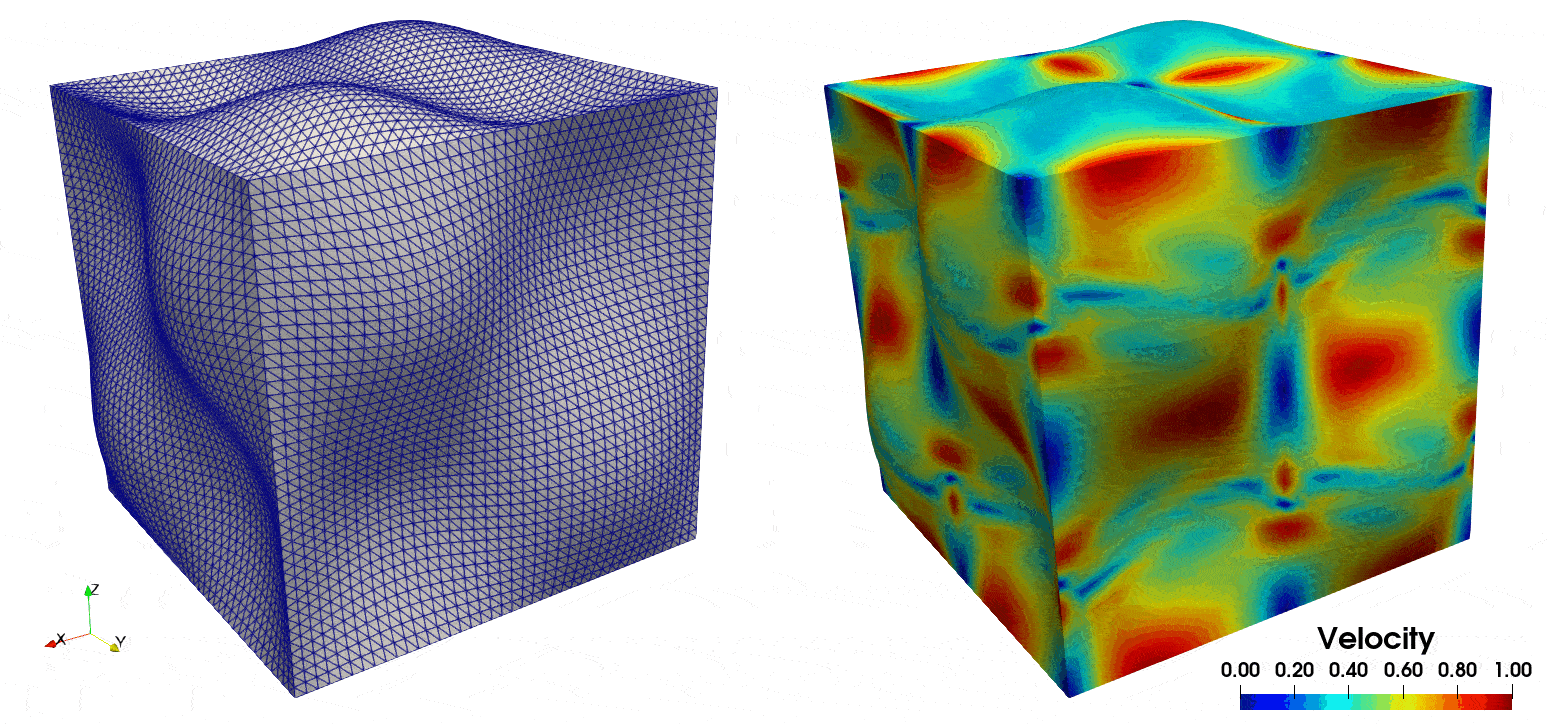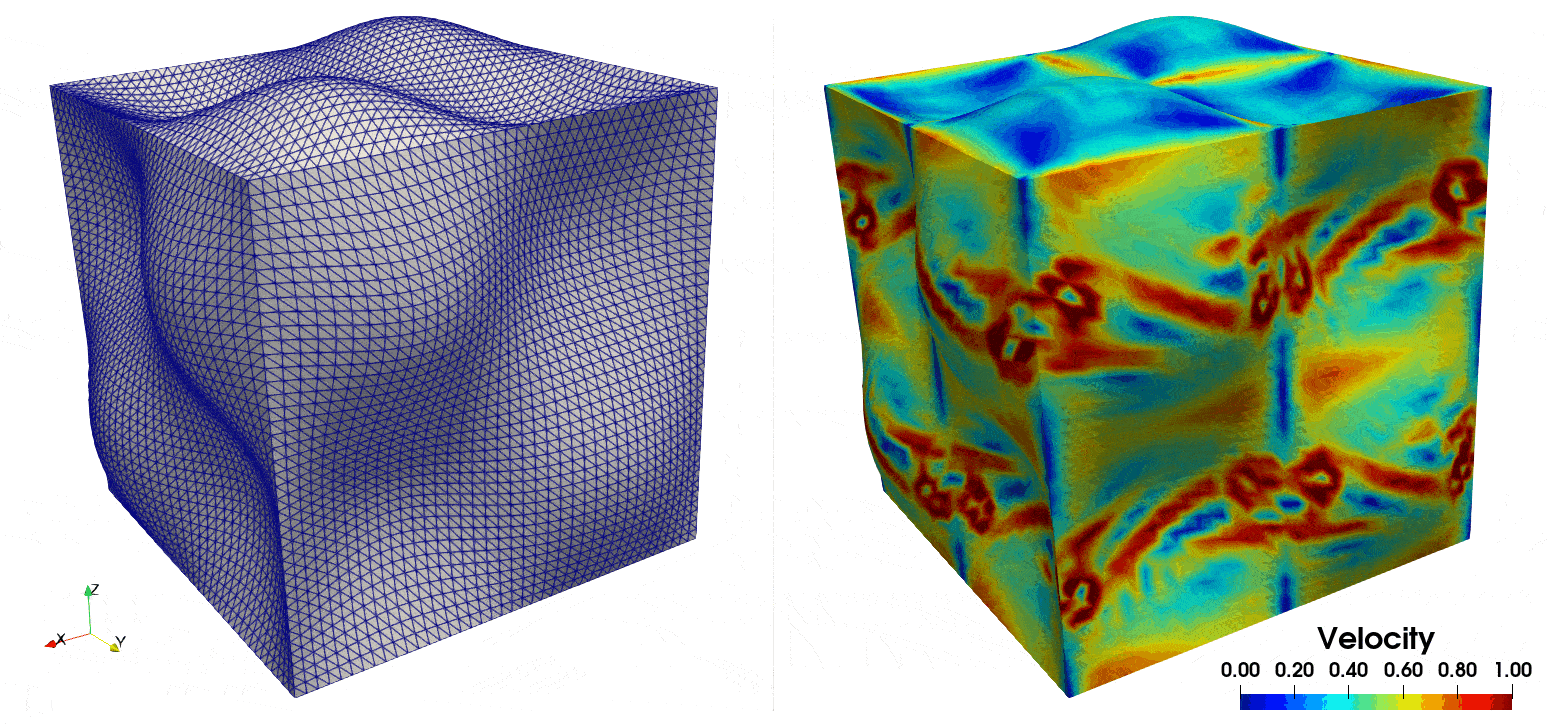
Fig. 8 On the left, the deforming cube geometry, and on the right the corresponding velocity field solution.

Increasing the spatial resolution in 3D

Similar to the moving vortex, the default resolution for the Taylor-Green vortex in 3D is a cube with resolution parameters \(N_x=32\), \(N_y=32\), and \(N_z=32\). In contrast to the 2D moving vortex problem, the number of tetrahedral cells are now computed using the following formula:

\[ \text{Number of tetrahedral cells } = 6\times N_x \times N_y \times N_z,\]

resulting in a total of 196 608 cells using the default parameters. To increase the mesh resolution, we can supply these parameters as command-line arguments to change their value. For instance, to create a mesh consisting of 750 000 cells, we can run the following command:

$ oasismove NSfracStepMove problem=MovingTaylorGreen3D Nx=50 Ny=50 Nz=50

FHWK21

Niklas Fehn, Johannes Heinz, Wolfgang A Wall, and Martin Kronbichler. High-order arbitrary lagrangian–eulerian discontinuous galerkin methods for the incompressible navier–stokes equations. Journal of Computational Physics, 430:110040, 2021.

TG37

Geoffrey Ingram Taylor and Albert Edward Green. Mechanism of the production of small eddies from large ones. Proceedings of the Royal Society of London. Series A-Mathematical and Physical Sciences, 158(895):499–521, 1937.