Backflow stabilization

Here we demonstrate simulation divergence due to backflow, and how we can stabilize the flow to prevent this in OasisMove, based on the first backflow stabilization method tested by Moghadam et al. [EMBH+11]. To demonstrate this we will be investigating parabolic flow through an eccentric stenosis model in two-dimensions. The setup is inspired by the three-dimensional study of stenotic flow by Varghese et al. [VFF07], who consider a longer stenosis model than presented here. Note that this is not a moving domain simulation, but the implementation of backflow stabilization is general, and works for both rigid and moving domains.

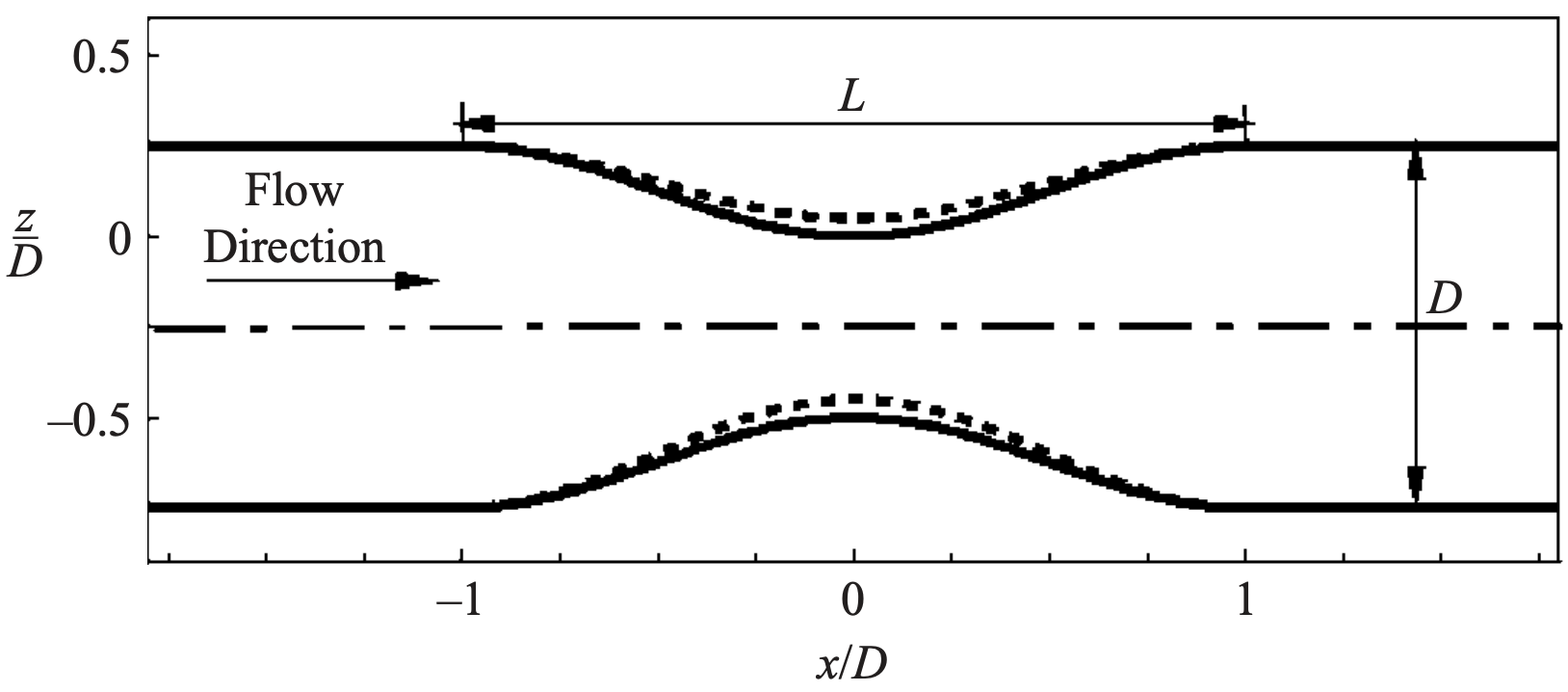
Fig. 9 A schematic of the two-dimensional stenosis model with a slight eccentricity of the stenosis, borrowed from Varghese et al.

Problem description

The problem consists of a two-dimensional stenosis, which is constructed based on its (dimensionless) diameter \(D\). In this example we set \(D=6.35\), and let the length of the stenosis be \(L=2D\), as shown Fig. 9, while the domain \(\Omega\) is defined as \(\Omega = [x_0D, x_1D]\times[-D/2, D/2]\), where \(x_0\) and \(x_1\) are scalar factors, which adjust the length of the domain. At the inlet a constant parabolic velocity profile is prescribed with maximum velocity \(U_0\), while the outlet is considered an open boundary with a zero pressure boundary condition. A visualization of the triangulated mesh, and a zoomed in view on the stenosis is shown in Fig. 10.

Fig. 10 The computational domain for the eccentric stenosis with the default resolution \(N=50\). On the left, an overview of the domain, and on the right, a zoomed in view of the stenosis.

Furthermore, the simulation with default parameters is run for a Reynolds number equal to \(Re=2540\), which is adjustable in the problem file Stenosis.py, either by changing the kinematic viscosity \(\nu\), the cylinder diameter \(D\), or the maximum velocity \(U_0\).

Backflow stabilization in OasisMove

This problem is intended to demonstrate how to prevent backflow divergence. Simulation divergence due to backflow is a rather common in cardiovascular flows, particularly in blood flow in large vessels or at the mitral valve orifice in the left atrium. Because backflow is a naturally occurring physiologic phenomenon, careful treatment is necessary to realistically model backflow without artificially altering the local flow dynamics. To achieve this we consider the first backflow stabilization method first proposed by Bazilevs et al. [BGH+09] and rigorously tested by Moghadam et al. In short, the method modifies the weak formulation of the Navier-Stokes equations by adding a backflow stabilization term for the Neumann boundaries, in this case the outlet. Specifically, the following convective traction term is added to the weak form on each Neumann boundary to be stabilized:

(13)\[ -\beta \int_{\partial \Omega} (\mathbf u \cdot \mathbf n)\_\mathbf u \cdot \mathbf v \, \text{d}s,\]

where \(\beta\) is a positive coefficient between 0.0 and 1.0, \(\mathbf u\) is the velocity vector, \(\mathbf v\) is the velocity test function, \(\partial \Omega\) denotes the boundary, and \((\mathbf u \cdot \mathbf n)\_\) is defined as:

(14)\[ (\mathbf u \cdot \mathbf n)\_ \,=\, \frac{\mathbf u\cdot \mathbf n - \| \mathbf u \cdot \mathbf n\|}{2}.\]

In OasisMove, the backflow stabilization method is applied by supplying the backflow_facets argument, in addition to the backflow_beta parameter. The backflow_beta parameter determines the strength of the stabilization term and can be any float value between 0.0 and 1.0, while backflow_facets represents a list of IDs corresponding to the boundary IDs of the Neumann boundaries. For the stenosis problem, where the outlet boundary ID is 3, backflow stabilization can be added to the outlet with a strength of 0.2 by running the following command:

$ oasismove NSfracStep solver=IPCS_ABCN problem=Stenosis backflow_facets="[3]" backflow_beta=0.2 

Note that the list of boundaries has to be encapsulated by quotation marks, or the IDs can be manually set inside Stenosis.py. Note also that backflow stabilization in OasisMove is currently only implemented for the IPCS_ABCN and IPCS_ABCN_Move solvers.

Simulation in OasisMove

To run the stenosis problem for \(T=15\) with default parameters in OasisMove, which by defaut includes backflow stabilization at the outlet, you can run the following command:

$ oasismove NSfracStep solver=IPCS_ABCN problem=Stenosis 

where we specify the NSfracStep module and IPCS_ABCN solver because the problem is not moving. Alternatively we can pass the dynamic_mesh=False flag for rigid domain problems, telling the default solver (IPCS_ABCN_Move) to skip solving the mesh equations:

$ oasismove NSfracStepMove problem=Stenosis dynamic_mesh=False 

The default time step is set to \(T=15\) and might take some minutes to complete, depending on your hardware. Alternatively, you can solve the problem in parallel to speed up the simulation time:

$ mpirun -np 8 oasismove NSfracStepMove problem=Stenosis dynamic_mesh=False 

Results

When the simulation is finished, there will be a folder named results_stenosis, which contains the velocity and pressure solution in .xdmf format. In Fig. 11 we display the resulting velocity field without (top) and with (bottom) backflow stabilization, where we have added vectors scaled by the velocity magnitude. Note that the simulation without stabilization diverges at approximately \(T=14\), while the stabilized simulation keeps running until \(T=50\).

Fig. 11 The velocity field for the stenosis problem without (top) and with (bottom) backflow stabilization, including vector arrows that have been scaled by the velocity magnitude.

BGH+09

Y Bazilevs, JR Gohean, TJR Hughes, RD Moser, and Y25718211229 Zhang. Patient-specific isogeometric fluid–structure interaction analysis of thoracic aortic blood flow due to implantation of the jarvik 2000 left ventricular assist device. Computer Methods in Applied Mechanics and Engineering, 198(45-46):3534–3550, 2009.

EMBH+11

Mahdi Esmaily Moghadam, Yuri Bazilevs, Tain-Yen Hsia, Irene E Vignon-Clementel, Alison L Marsden, and Modeling of Congenital Hearts Alliance (MOCHA). A comparison of outlet boundary treatments for prevention of backflow divergence with relevance to blood flow simulations. Computational Mechanics, 48:277–291, 2011.

VFF07

Sonu S Varghese, Steven H Frankel, and Paul F Fischer. Direct numerical simulation of stenotic flows. part 1. steady flow. Journal of Fluid Mechanics, 582:253–280, 2007.