Vortex problem with oscillating boundaries

In this tutorial we will consider a two-dimensional moving vortex problem inspired by the Taylor-Green vortex problem, introduced in [HW07]. The problem is implemented in the file MovingVortex.py, but note that it has not been optimized for parallelization because of its intended use for code verification.

Problem description

The problem has an analytical solution of the two-dimensional incompressible Navier–Stokes equations in the absence of body forces, \(\mathbf{f} = 0\), namely:

(8)\[\begin{split} \mathbf u(\mathbf x,t) &= (-\sin (2\pi x_2), \sin(2\pi x_1))e^{-4\nu \pi^2 t}\\ p(\mathbf x,t) &= -\cos(2\pi x_1)\cos(2\pi x_2)e^{-8\nu \pi^2 t}\end{split}\]

where \(\mathbf x = (x_1, x_2)\) are the Euclidean coordinates, and \(\nu = 0.025\) \(\text{m}^2\)/s. Furthermore, the mesh velocity \(\mathbf w\) is determined by the following displacement field:

(9)\[\begin{split} \mathbf x(\mathbf X , t) &= \chi + A_0 \sin \left(\frac{2 \pi t}{T_G}\right) \left(\sin\left(2\pi \frac{\chi_2 + L / 2}{L}\right),\sin\left(2\pi \frac{\chi_1 + L / 2}{L}\right)\right)\\ \mathbf w(\mathbf X , t) &= \frac{\partial \mathbf x}{\partial t}\end{split}\]

where \(\mathbf X= (X_1, X_2)\) are the ALE coordinates, \(A_0=0.08\) is the amplitude, \(T_G=4T\) is the period length of the mesh motion, \(T\) is the length of one cycle, and \(L=1\).

Simulation in OasisMove

To simulate this flow problem in OasisMove using the default parameters you can run the following command:

$ oasismove NSfracStepMove problem=MovingVortex 

and the simulation will start. The simulation should only take a couple of seconds when running with the default parameters, as it is run on a relatively coarse mesh for only 20 time steps.

Results

When the simulation is finished, there will be a folder named results_moving_vortex, in the current working directory. The results-folder contains all simulation results per run. Running the moving vortex problem with the default parameters should produce three solution files located in the Solutions folder: velocity.xdmf, pressure.xdmf, and the exact velocity solution velocity_exact.xdmf. These solution files can be visualized in ParaView or any similar visualization software, and in Fig. 7 we display the displaced grid, velocity and pressure solution at \(T=1\).

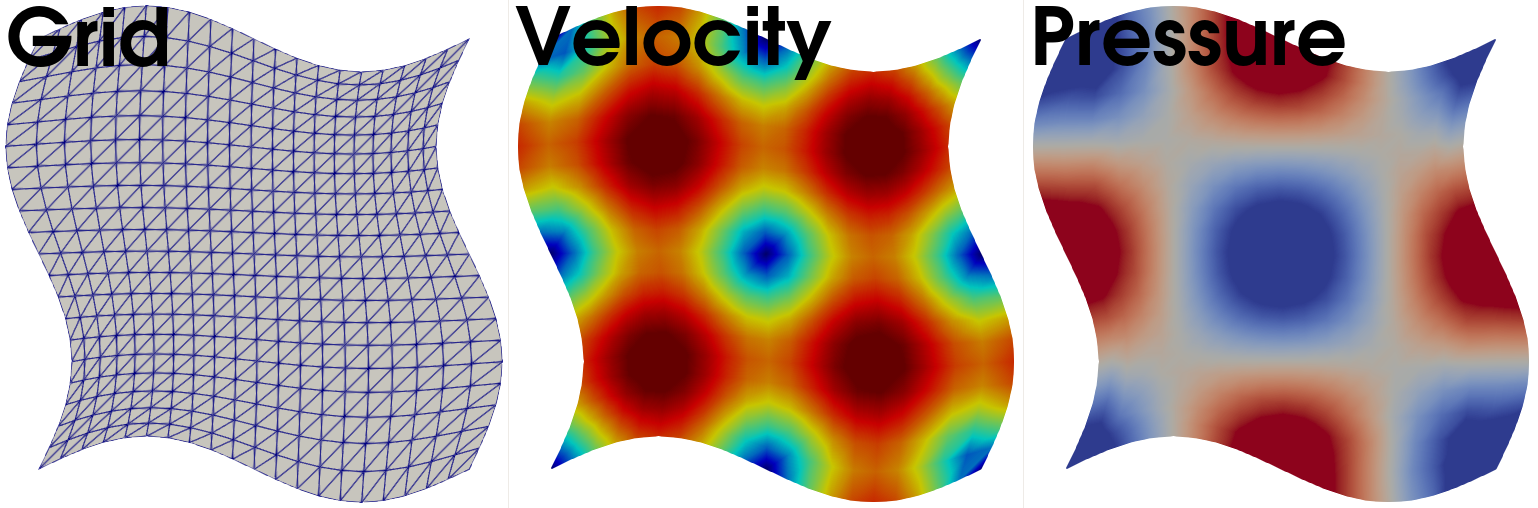
Fig. 7 From left to right: The grid displacement, velocity solution and pressure field at \(T=1\).

Increasing the spatial and temporal resolution

The default resolution for the vortex problem is using the resolution parameters \(N_x=20\) and \(N_y=20\) resulting in \(2\times N_x \times N_y = 800\) triangular cells in the mesh. To increase the mesh resolution, we can supply these parameters as command-line arguments to change their value. For instance, to create a mesh consisting of 20000 cells, we can run the following command:

$ oasismove NSfracStepMove problem=MovingVortex Nx=100 Ny=100

Similarly, we can adjust the number of time steps the simulation should perform by adjusting the time step parameter dt, which by default is \(\Delta t = 5\cdot 10^{-2}\). To simulate 1000 time steps between \(t=0\) and \(t=T=1\), we can run the following command:

$ oasismove NSfracStepMove problem=MovingVortex T=1 dt=0.001

Important

When adjusting spatial and temporal resolution is important to know relationship between the cell size and the time-step size, which are closely related through the Courant number (\(C\)) given by the Courant-Friedrichs-Lewy (CFL) condition:

(10)\[ C ={\frac {u\,\Delta t}{\Delta x}} < C_{\max }, \]

where \(u\) is the velocity magnitude, \(\Delta t\) is the time step size, and \(\Delta x\) is the length interval. The general consensus is that \(C_{\max} = 1\).

HW07

Jan S Hesthaven and Tim Warburton. Nodal discontinuous Galerkin methods: algorithms, analysis, and applications. Springer Science & Business Media, 2007.